DornTorus - „Eine Geometrie für Alles”
Erste Schritte
Seite: 1 2 3 4 5 6 7 8 9 (für Physiker) / Original-Text, © 1996...2000 / dieses Update als pdf (→Druckversion) , © 2000 und 2017 Wolfgang W. Däumler (→ worum geht es hier ?)
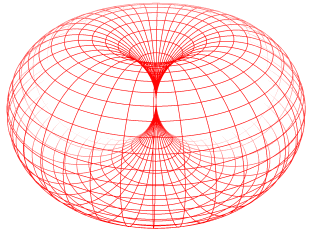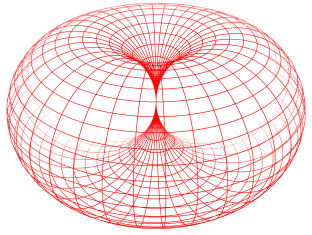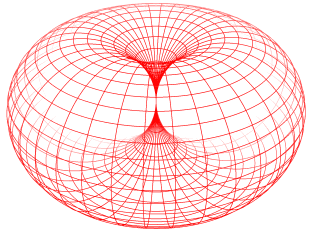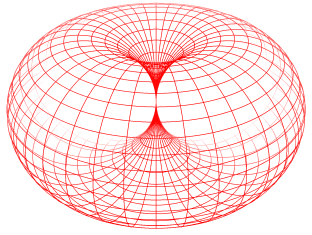
Die geometrische Figur Dorntorus (s.u.) soll nur Vorstellungshilfe bei der bildlichen Darstellung komplexer Zahlen sein, mehr zunächst nicht!Komplexe Zahlen sind Entitäten mit zwei voneinander unabhängigen Eigenschaften oder - umgangssprachlich - Größen (Real- und Imaginärteil), und auf genau solche „dualen” Entitäten sollen physikalische Objekte („Teilchen” mit „Wechselwirkungen” untereinander) mit Hilfe des DornTorus-Modells zurückgeführt werden.
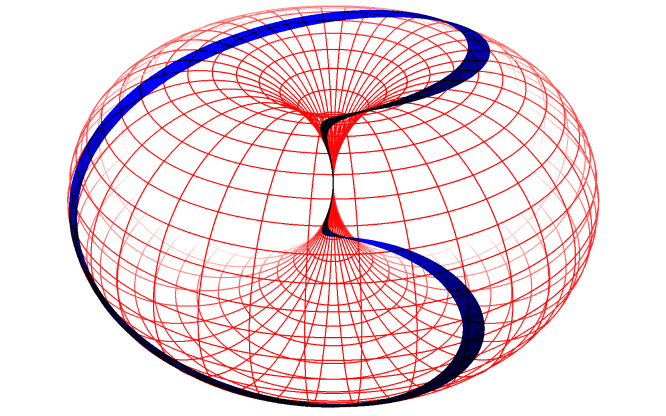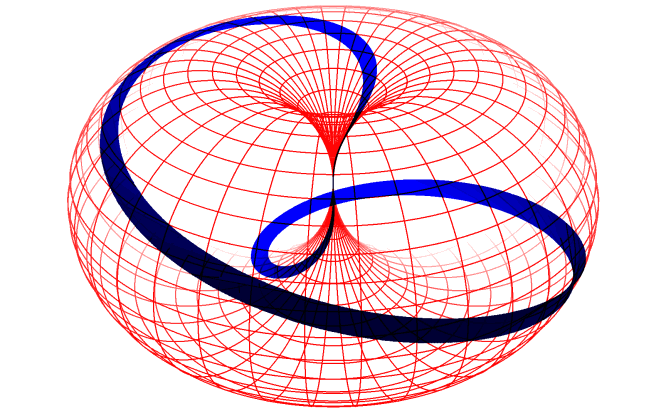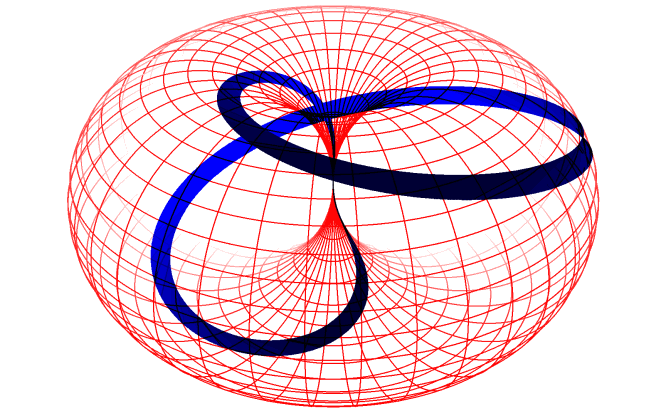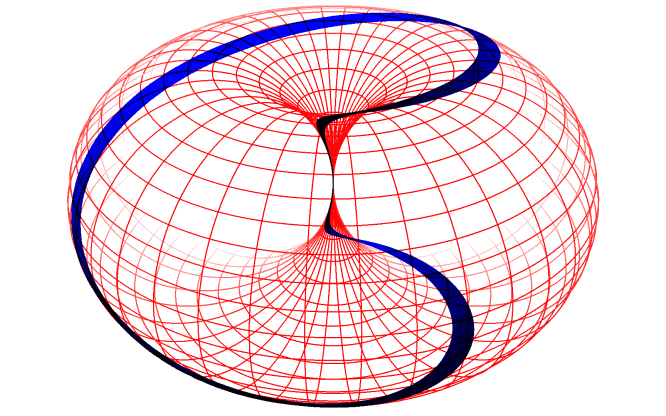
Das DornTorus-Bild bietet die Möglichkeit, aus nur zwei unabhängigen Eigenschaften sehr komplexe Strukturen zu erzeugen: Trajektorien („Abrolllinien” oder auch Zykloiden), die ein Punkt auf der Dorntorus-Oberfläche hinterlässt, wenn der Dorntorus rotiert und gleichzeitig seine Größe ändert, indem er sich entlang der Haupt-Symmetrieachse in Form einer wulstförmigen Umdrehung abrollt. (Eigenschaft 1: Rotation, Eigenschaft 2: Größe)
Diese Strukturen sind aber nicht in einen vorbestehenden (z.B. dreidimensionalen) Raum einzubetten. Die (im Raum der Anschauung „verwundenen”) Trajektorien sind die Koordinaten, die einen Raum aufspannen, dessen Dimensionszahl also der Zahl beteiligter Entitäten entspricht. Auf den Dimensionsbegriff kann man dann auch verzichten. Eine wirklich fundamentale Beschreibung der „Naturvorgänge” muss im übrigen auf alle vorbestehende Voraussetzungen verzichten, also auch auf unseren Raum der Anschauung inklusive Zeit und eben den Dimensionsbegriff. Die rein mathematische Konstruktion eines mehrdimensionalen Raumes mit einer Metrik erfordert bereits über 20 Axiome! Das ist alles andere als fundamental.
Gängige Physik, auch die „Theoretische Physik” ist immer anwendungsbezogen und muss experimentell „bestätigbar” sein (genauer: darf nicht falsifizierbar sein). Diese Bestätigung erfolgt allerdings stets im Rahmen unserer allgemein akzeptierten puren Vorstellung von Raum und Zeit, die genau genommen nicht genügend hinterfragt wird. Heutige Physik ist zwar fantastisch präzise und erlaubt exakte nachprüfbare Voraussagen, sie ist jedoch in erkenntnistheoretischem Sinn nicht fundamental, und sie erlaubt keine Schlüsse auf die Verhältnisse außerhalb unseres Vorstellungsraumes, weder bei sehr kleinen noch sehr großen Maßstäben.
Philosophische Betrachtungen und kontemplative Überlegungen zu - in epistemologischem Sinn - fundamentalen Gesetzen sind zwar „nur” Gedankenspielereien mit Analogmodellen, sie können aber durchaus - ohne gigantische Technik - Erkenntnisse erzeugen und beglückende Aha-Erlebnisse hervorrufen:
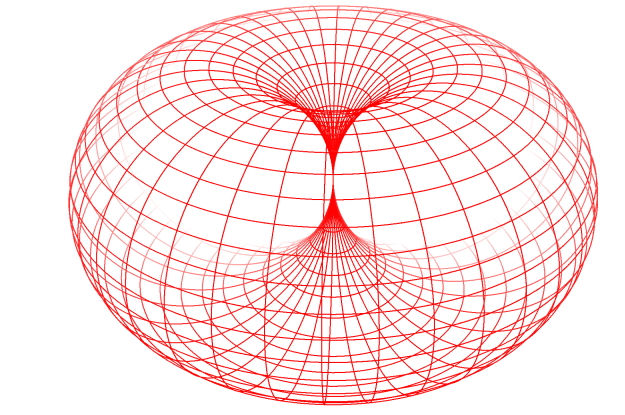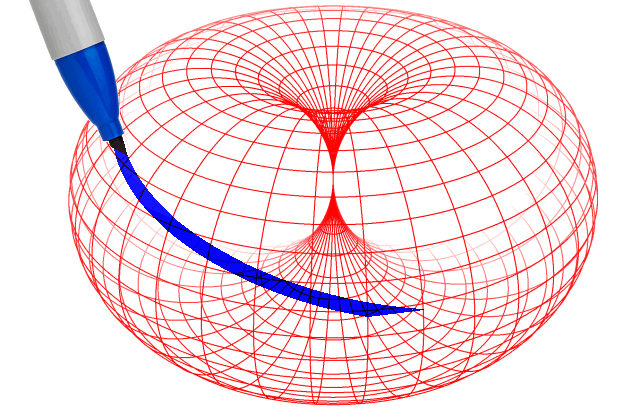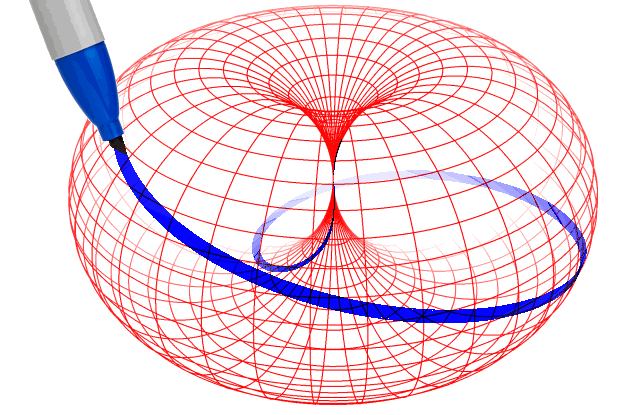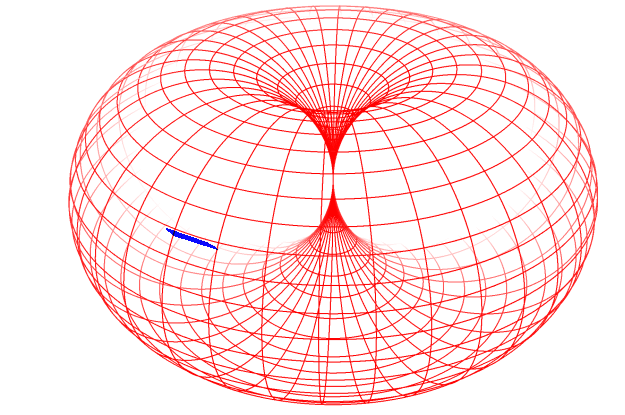
In einem ersten, sehr groben Bild kann man die geschlossenen, sich selbst überlagernden (Lissajous-)Figuren („Resonanzen”) auf der Dorntorus-Oberfläche als Fermionen interpretieren, und die nicht geschlossenen Linien dazwischen, die in ihrem Verlauf die gesamte Dorntorus-Oberfläche bedecken können, repräsentieren dann die Austauschbosonen zwischen „benachbarten” Fermionen.
Auf diese Weise beinhaltet eine einzige Entität alle möglichen „Teilchen”, in schöner Folge hintereinander aufgereiht und mit einer einzigen fortlaufenden und stetigen Kurve darstellbar, wie in dieser Animation grob gezeigt. (Detailausschnitte: photon/electron und nucleon/gluon/quarks)
Das Wechselspiel zweier oder mehrerer oder vieler Entitäten wird dargestellt durch „Ineinanderschachteln” zweier oder mehrerer oder vieler Dorntori, indem ihre Haupt-Symmetrieachsen und Mittelpunkte zusammenfallen, so dass sich dort Meridiane aller ineinander geschachtelten Tori berühren (s. Bild).
Sodann stelle man sich vor, die Dorntori rollen alle zusammen entlang ihrer gemeinsamen Symmetrieachse, z.B. von oben nach unten wie in dieser Animation. Genauso gut kann man die Tori sich aneinander, entlang ihrer Meridiane, abrollen sehen, mit jeweils gleicher Umfangsgeschwindigkeit und - je nach Größe - unterschiedlicher Winkelgeschwindigkeit (reziproke Eigenschaft 2), wie es in der Animation und den dortigen weiter führenden Links erkennbar ist.
Das Bild kompliziert sich drastisch, wenn die sich aneinander abrollenden Dorntori auch noch um ihre Haupt-Symmetrieachse rotieren, teils „rechts”, teils „links” herum. Jetzt rollen die Tori sich nicht mehr an Meridianen ab, sondern jeweils an den Trajektorien der resultierenden Bewegung (Rotieren und Abrollen kombiniert). Am Berührungspunkt, an der dünnsten Stelle des fadenförmigen Dorns, sind auch diese Linien „parallel”, im Sinne von Tangenten. Das Abrollen der Trajektorien statt der Meridiane aneinander hat Auswirkungen auf die Rotationsgeschwindigkeit (Eigenschaft 1) bei gleich bleibend angenommener Abrollgeschwindigkeit, wenn es - bildlich - sozusagen ohne „Schlupf” stattfinden soll.
Wir haben schon jetzt, mit einfachsten Mitteln, ein hoch komplexes und wahnsinnig interessantes System entwickelt! Vor dem Weiter-Denken ist aber ein Innehalten zu empfehlen und intensives Vertrautmachen mit der Geometrie des dynamischen DornTorus (© 1996-2000) resp.